Skip to contents

Variable Importance

Source: vignettes/articles/variable-importance.Rmd
variable-importance.Rmd

Intro

In the previous articles you have learned how to prepare the data for the analysis, how to train a model, how to make predictions, how to evaluate a model and two different evaluation strategies using SDMtune. In this article you will learn how to display and plot the variable importance and how to plot the response curves.

Variable importance for Maxent models

First we load the SDMtune package:

library(SDMtune)
#> 
#>    _____  ____   __  ___ __
#>   / ___/ / __ \ /  |/  // /_ __  __ ____   ___
#>   \__ \ / / / // /|_/ // __// / / // __ \ / _ \
#>  ___/ // /_/ // /  / // /_ / /_/ // / / //  __/
#> /____//_____//_/  /_/ \__/ \__,_//_/ /_/ \___/  version 1.3.2
#> 
#> To cite this package in publications type: citation("SDMtune").

For a Maxent model we can get the variable importance values from the output of the MaxEnt Java software. These values are stored in the model object and can be displayed using the following command:

default_model@model@results
X.Training.samples 400.0000
Regularized.training.gain 1.0331
Unregularized.training.gain 1.0959
Iterations 500.0000
Training.AUC 0.8728
X.Background.points 5000.0000
bio1.contribution 83.9402
bio12.contribution 1.8103
bio16.contribution 0.3905
bio17.contribution 0.5052
bio5.contribution 0.9666
bio6.contribution 1.3898
bio7.contribution 0.3164
bio8.contribution 9.2951
biome.contribution 1.3858
bio1.permutation.importance 55.4917
bio12.permutation.importance 7.3454
bio16.permutation.importance 0.0200
bio17.permutation.importance 3.0841
bio5.permutation.importance 6.4903
bio6.permutation.importance 1.1164
bio7.permutation.importance 2.9769
bio8.permutation.importance 18.1317
biome.permutation.importance 5.3435
Entropy 7.4862
Prevalence..average.probability.of.presence.over.background.sites. 0.2172
Fixed.cumulative.value.1.cumulative.threshold 1.0000
Fixed.cumulative.value.1.Cloglog.threshold 0.0544
Fixed.cumulative.value.1.area 0.4232
Fixed.cumulative.value.1.training.omission 0.0100
Fixed.cumulative.value.5.cumulative.threshold 5.0000
Fixed.cumulative.value.5.Cloglog.threshold 0.2660
Fixed.cumulative.value.5.area 0.3340
Fixed.cumulative.value.5.training.omission 0.0450
Fixed.cumulative.value.10.cumulative.threshold 10.0000
Fixed.cumulative.value.10.Cloglog.threshold 0.3735
Fixed.cumulative.value.10.area 0.2876
Fixed.cumulative.value.10.training.omission 0.0750
Minimum.training.presence.cumulative.threshold 0.3722
Minimum.training.presence.Cloglog.threshold 0.0150
Minimum.training.presence.area 0.4990
Minimum.training.presence.training.omission 0.0000
X10.percentile.training.presence.cumulative.threshold 11.9719
X10.percentile.training.presence.Cloglog.threshold 0.4072
X10.percentile.training.presence.area 0.2734
X10.percentile.training.presence.training.omission 0.1000
Equal.training.sensitivity.and.specificity.cumulative.threshold 24.7858
Equal.training.sensitivity.and.specificity.Cloglog.threshold 0.5691
Equal.training.sensitivity.and.specificity.area 0.2074
Equal.training.sensitivity.and.specificity.training.omission 0.2075
Maximum.training.sensitivity.plus.specificity.cumulative.threshold 10.9491
Maximum.training.sensitivity.plus.specificity.Cloglog.threshold 0.3900
Maximum.training.sensitivity.plus.specificity.area 0.2806
Maximum.training.sensitivity.plus.specificity.training.omission 0.0775
Balance.training.omission..predicted.area.and.threshold.value.cumulative.threshold 1.4303
Balance.training.omission..predicted.area.and.threshold.value.Cloglog.threshold 0.0864
Balance.training.omission..predicted.area.and.threshold.value.area 0.4016
Balance.training.omission..predicted.area.and.threshold.value.training.omission 0.0100
Equate.entropy.of.thresholded.and.original.distributions.cumulative.threshold 3.3019
Equate.entropy.of.thresholded.and.original.distributions.Cloglog.threshold 0.1993
Equate.entropy.of.thresholded.and.original.distributions.area 0.3566
Equate.entropy.of.thresholded.and.original.distributions.training.omission 0.0300

The function maxentVarImp() extracts the variable importance values from the previous output and formats them in a more human readable way:

vi <- maxentVarImp(default_model)
vi
Variable Percent_contribution Permutation_importance
bio1 83.9402 55.4917
bio8 9.2951 18.1317
bio12 1.8103 7.3454
bio6 1.3898 1.1164
biome 1.3858 5.3435
bio5 0.9666 6.4903
bio17 0.5052 3.0841
bio16 0.3905 0.0200
bio7 0.3164 2.9769

As you can see the function returns a data.frame with the variable name, the percent contribution and the permutation importance.

You can plot the variable importance as a bar chart using the function plotVarImp(). For example you can plot the percent contribution using:

plotVarImp(vi[, 1:2])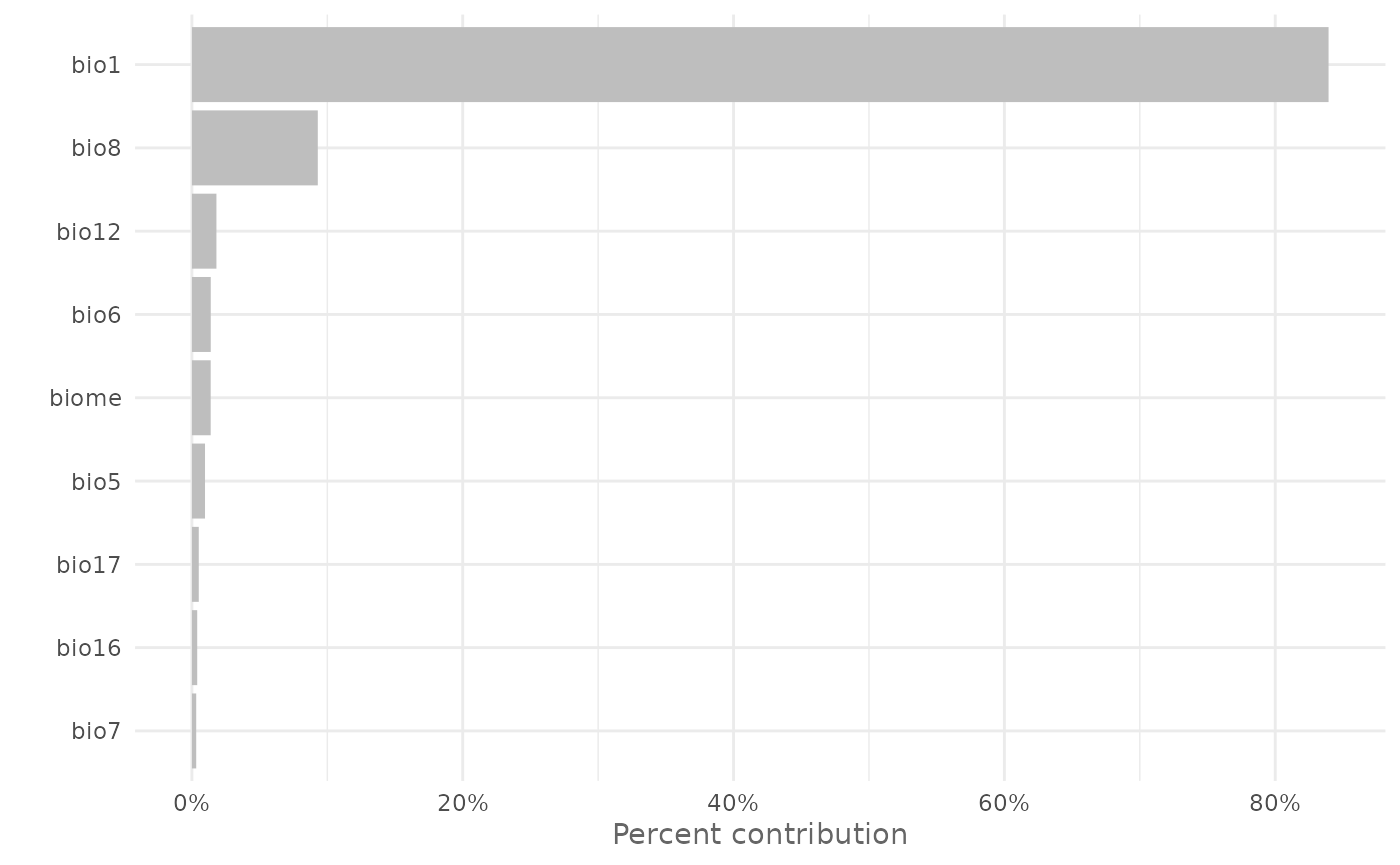

Try yourself

Plot the permutation importance as a bar chart. To see the solution highlight the following cell:

# The function accepts a data.frame with 2 columns: one with the variable name
# and one with the values, so it is enough to select the first and the third
# columns from the vi data.frame
plotVarImp(vi[, c(1,3)])

SDMtune has its own function to compute the permutation importance that iterates through several permutations and return an averaged value together with the standard deviation. We will use this function to compute the permutation importance of a Maxnet model.

Permutation importance

For this example we use a Maxnet model and a training/testing validation strategy like in the previous article:

library(zeallot)  # For unpacking assignment
c(train, test) %<-% trainValTest(data, 
                                 test = 0.2, 
                                 only_presence = TRUE, 
                                 seed = 25)

maxnet_model <- train("Maxnet", 
                      data = train)

Now we can calculate the variable importance with the function varImp() using 5 permutations:

vi_maxnet <- varImp(maxnet_model, 
                    permut = 5)
vi_maxnet
Variable Permutation_importance sd
bio1 55.4 0.015
bio8 20.4 0.007
biome 5.7 0.002
bio17 5.2 0.003
bio5 5.0 0.003
bio7 3.4 0.001
bio16 2.0 0.002
bio12 1.8 0.002
bio6 1.2 0.001

And plot it with:

plotVarImp(vi_maxnet)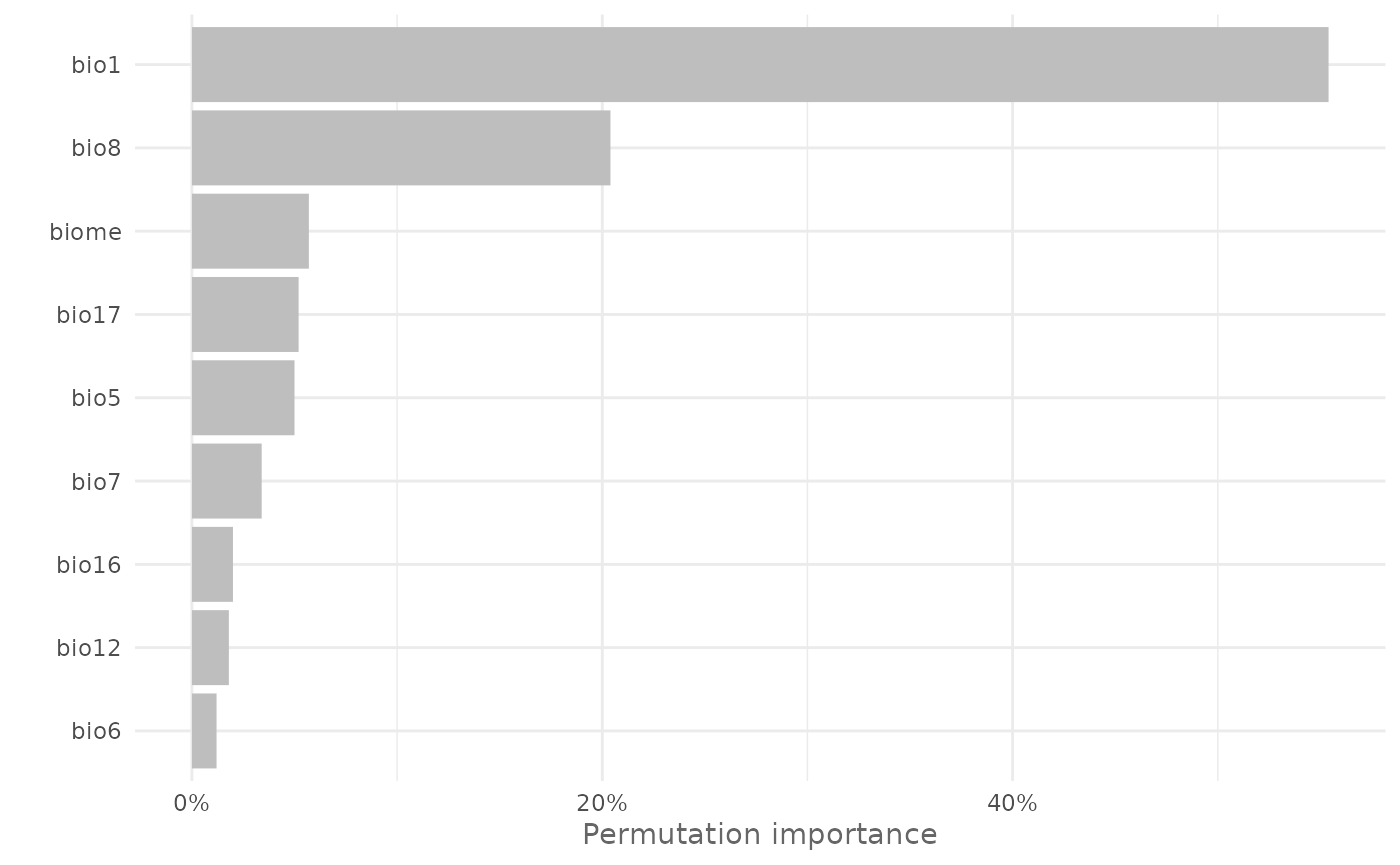

Try yourself

Use the varImp() function to compute the permutation importance for the default_model using 10 permutations and compare the results with the Maxent output. To see the solution highlight the following cell:

# Compute the permutation importance
vi_maxent <- varImp(default_model, 
                    permut = 10)

# Print it
vi_maxent

# Compare with Maxent output
maxentVarImp(default_model)

The difference is probably due to a different shuffling of the presence and background locations during the permutation process and because in this example we performed 10 permutations and averaged the values.

Jackknife test for variable importance

Another method to estimate the variable importance is the leave one out Jackknife test. The test removes one variable at time and records the change in the chosen metric. We use the function doJk(), the AUC as evaluation metric and the maxnet_model:

jk <- doJk(maxnet_model, 
           metric = "auc", 
           test = test)
jk
Variable Train_AUC_without Train_AUC_withonly Test_AUC_without Test_AUC_withonly
bio1 0.8697906 0.8470397 0.8477113 0.8451538
bio12 0.8748544 0.7383734 0.8500262 0.7497700
bio16 0.8749850 0.7435100 0.8510863 0.7795350
bio17 0.8748731 0.6149309 0.8491062 0.5770612
bio5 0.8752431 0.7307534 0.8518762 0.7067212
bio6 0.8743531 0.8195153 0.8509362 0.8325700
bio7 0.8741562 0.7271834 0.8488388 0.7420450
bio8 0.8668319 0.8319653 0.8480237 0.8246163
biome 0.8705269 0.7874897 0.8481788 0.7857500

We can also plot the output using the function plotJk(). In the following example we plot the previous result and we add a line representing the AUC of the full model trained using all the variables. First we plot the Jackknife test for the training AUC:

plotJk(jk, 
       type = "train", 
       ref = auc(maxnet_model))

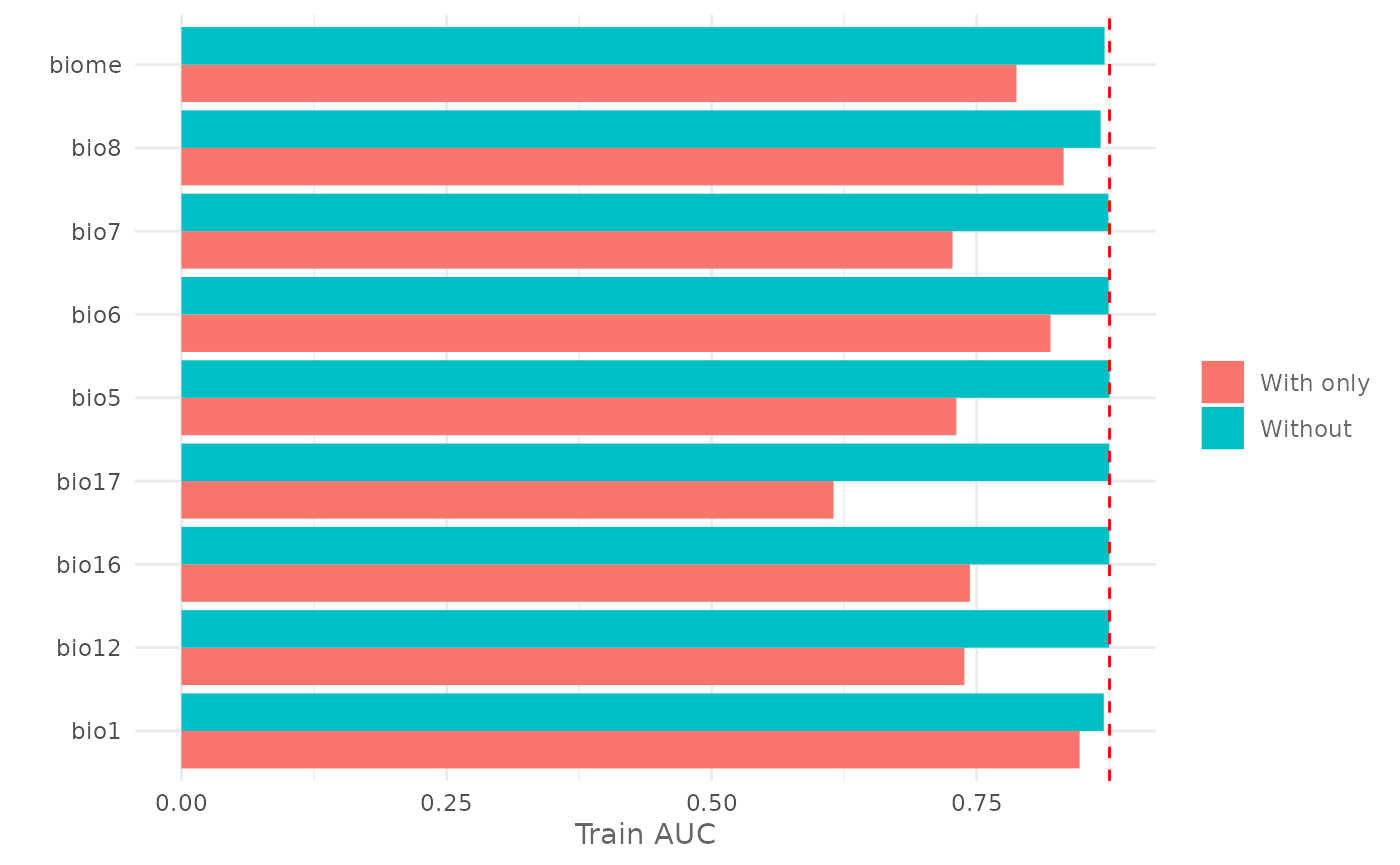
and the Jackknife test for the testing AUC:

plotJk(jk, 
       type = "test", 
       ref = auc(maxnet_model, test = test))

Try yourself

Repeat the Jackknife part using the TSS and the AICc as evaluation metric and using the dafult_model

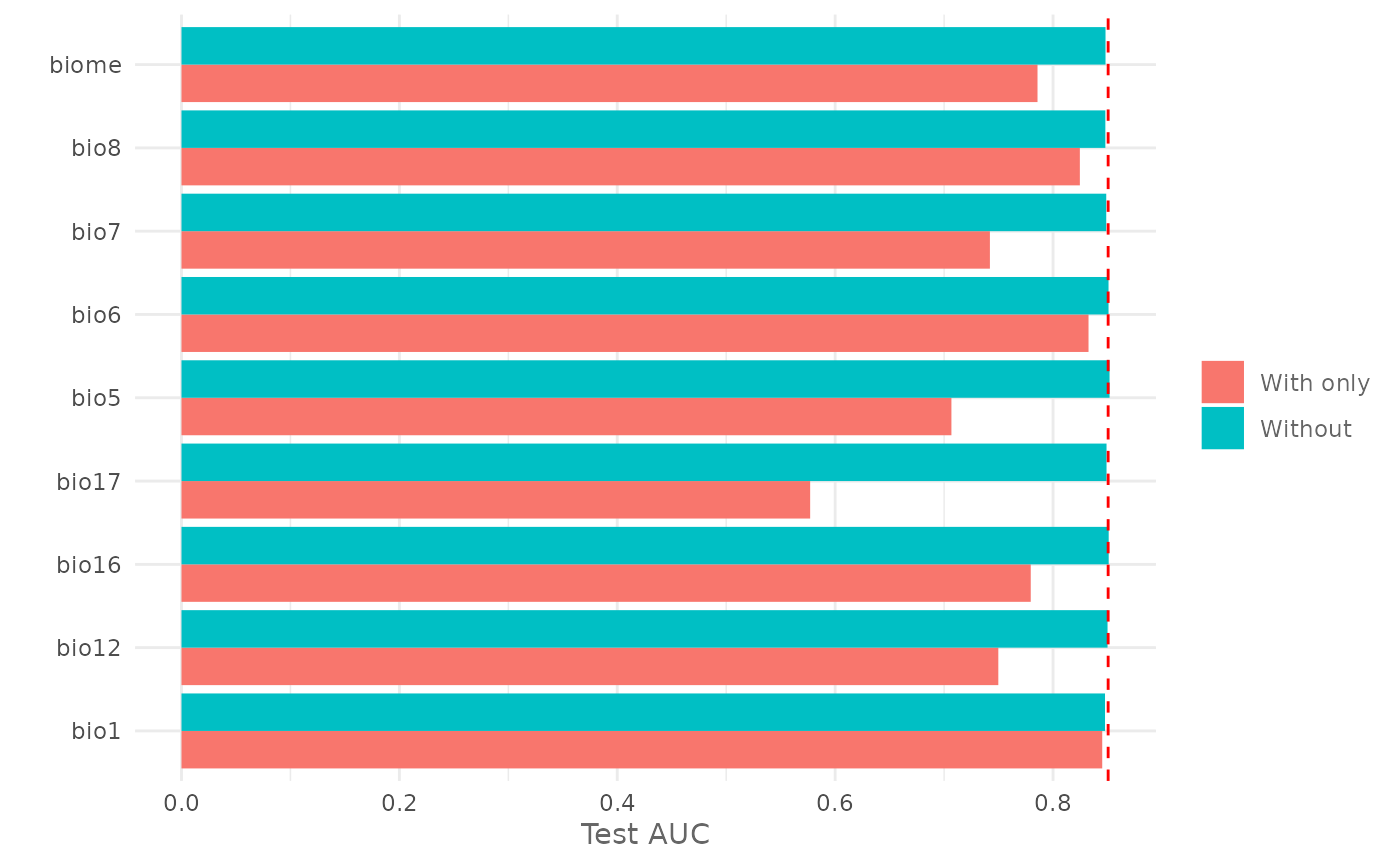
Response curves

With the function plotResponse() is possible to plot the marginal and the univariate response curve. Let’s plot the cloglog univariate response curve of bio1:

plotResponse(maxnet_model, 
             var = "bio1", 
             type = "cloglog", 
             only_presence = TRUE, 
             marginal = FALSE, 
             rug = TRUE)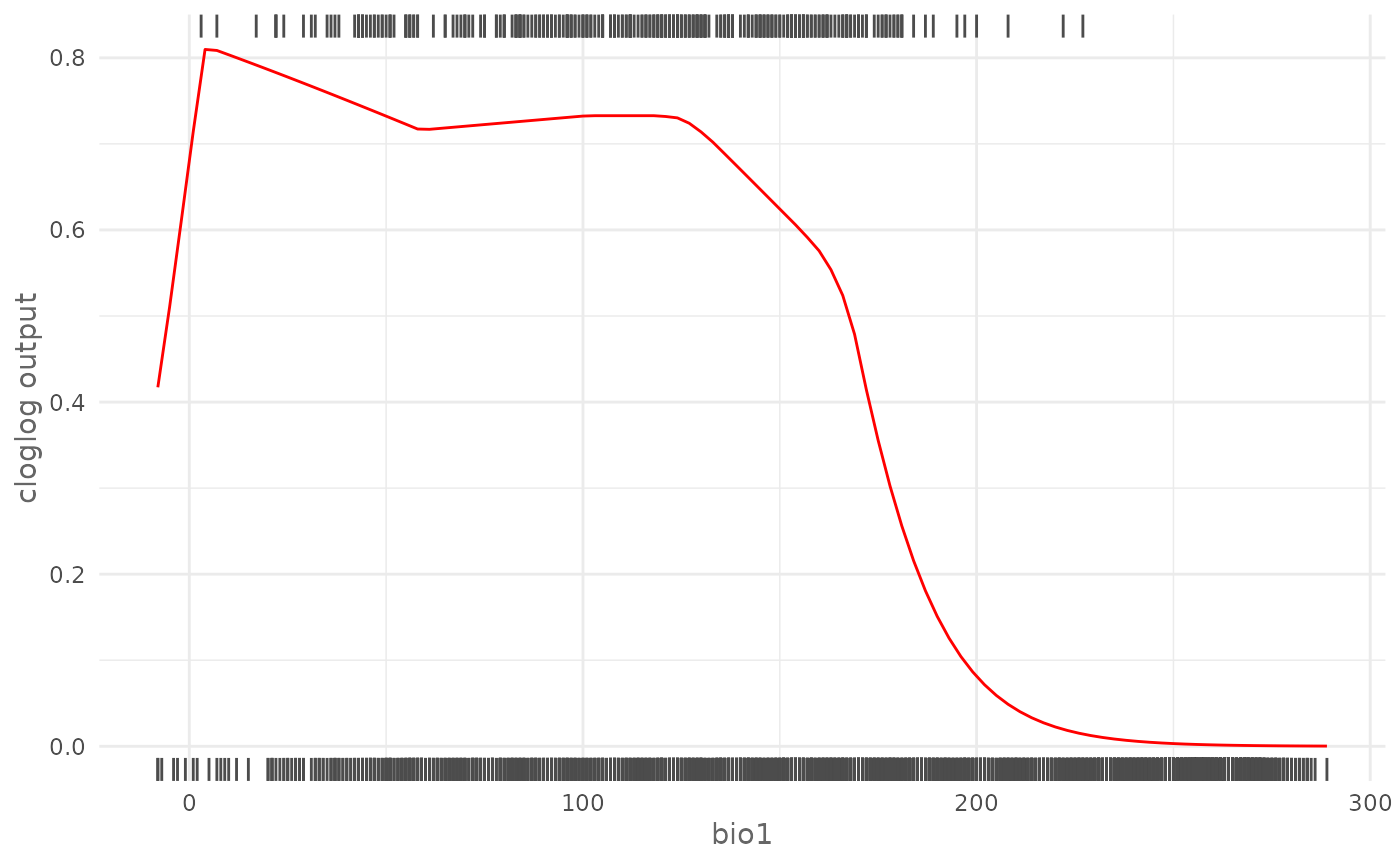

On top is displayed the rug of the presence locations and on bottom the rug of the background locations. As another example we can plot the logistic marginal response curve of biome that is a categorical variable, keeping the other variables at the mean value:

plotResponse(maxnet_model, 
             var = "biome", 
             type = "logistic", 
             only_presence = TRUE, 
             marginal = TRUE, 
             fun = mean, 
             color = "blue")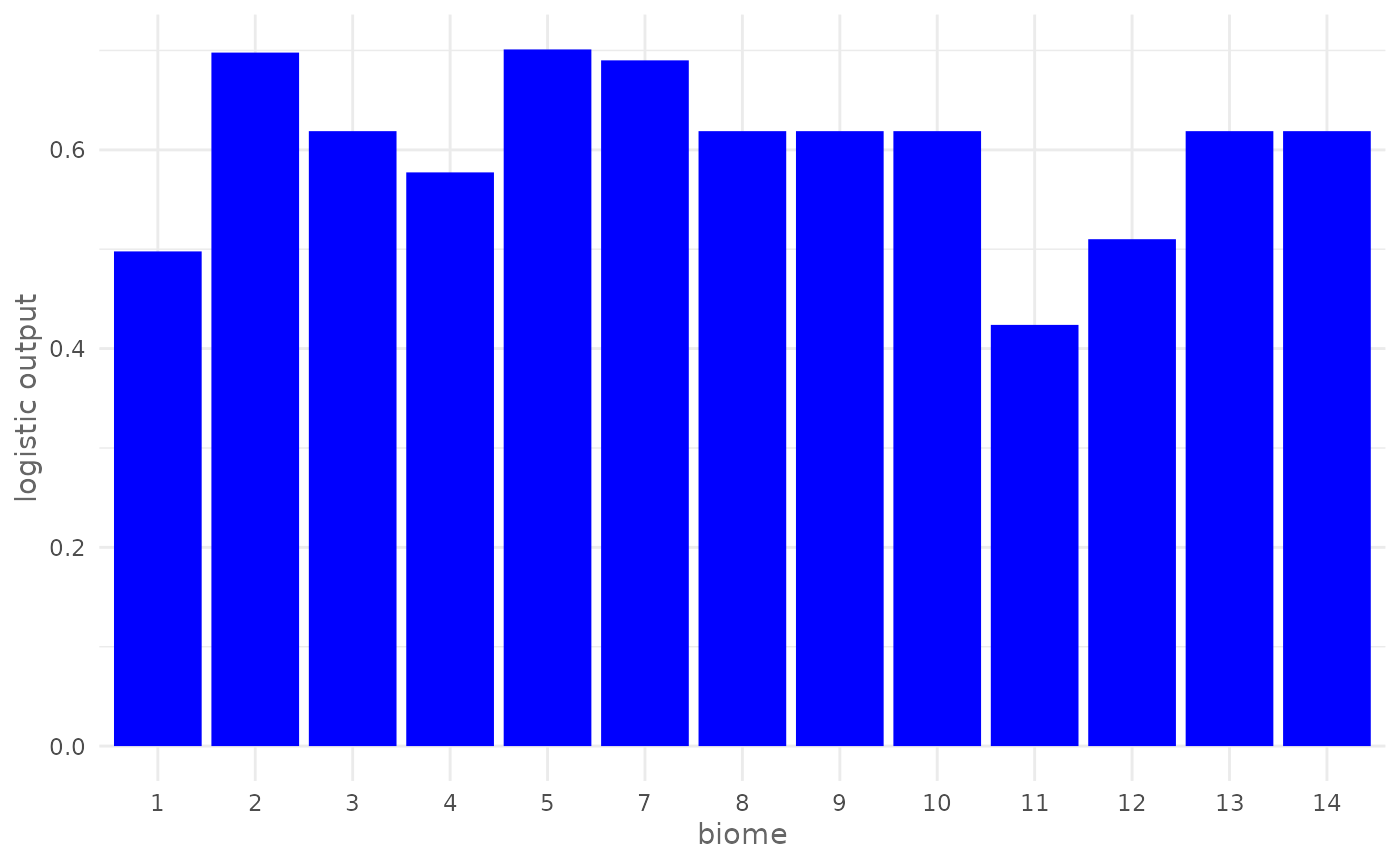

Try yourself

Plot in green the univariate cloglog response curve of bio17 removing the rug and using the default_model, to see the solution highlight the following cell:

plotResponse(default_model, 
             var = "bio17", 
             type = "cloglog", 
             only_presence = TRUE, 
             marginal = FALSE, 
             color = "green")

In the case of an SDMmodelCV() the response curve shows the averaged value of the prediction together with one Standard Deviation error interval. We use the cross validation model trained in the previous article:

plotResponse(cv_model, 
             var = "bio1", 
             type = "cloglog", 
             only_presence = TRUE, 
             marginal = TRUE, 
             fun = mean, 
             rug = TRUE)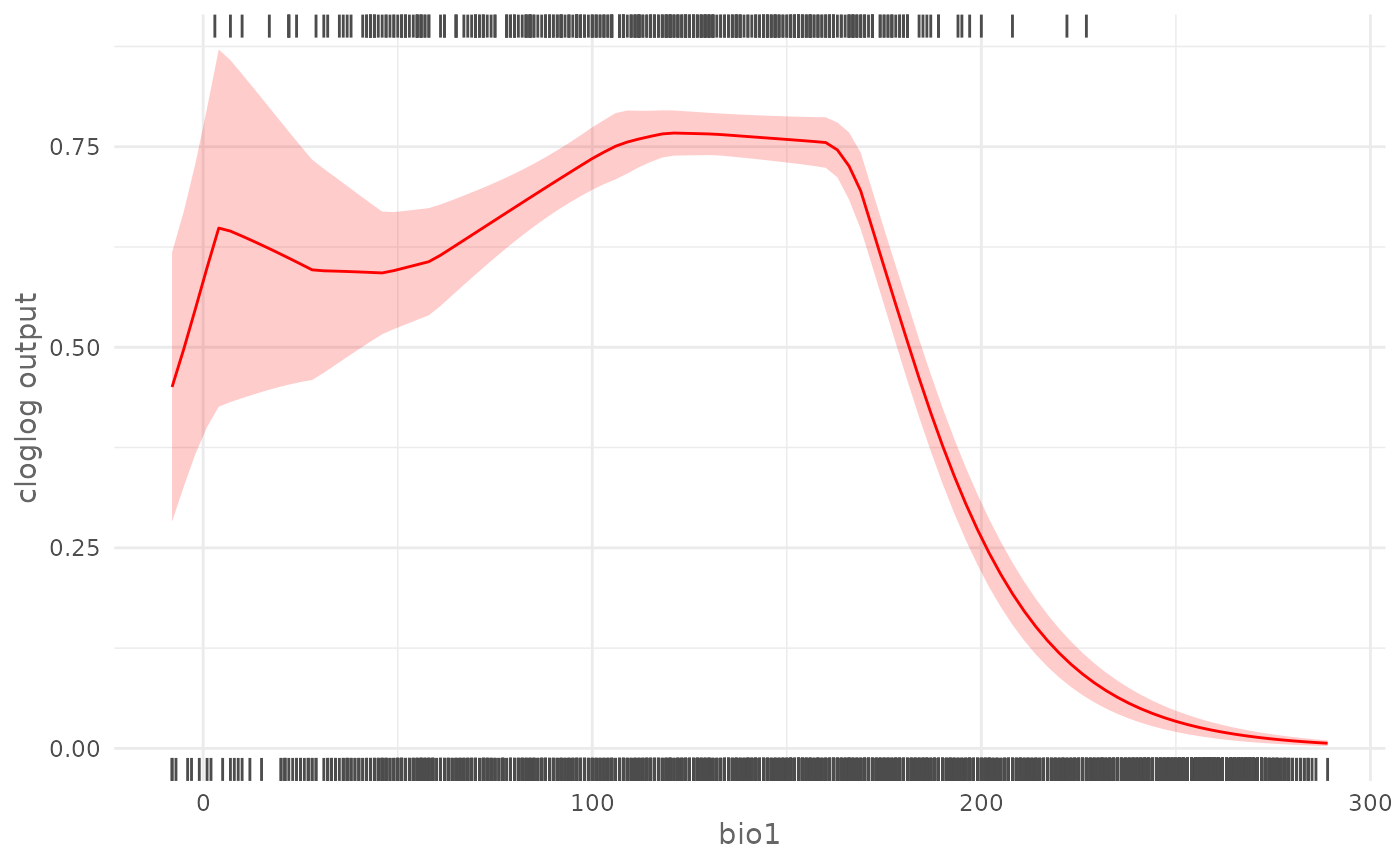

Model report

All what you have learned till now con be saved and summarized calling the function modelReport(). The function will:

  • save the training, background and testing locations in separated csv files;
  • train and evaluate the model;
  • create a report in a html format with the ROC curve, threshold values, response curves, predicted map and Jackknife test;
  • save the predicted distribution map;
  • save all the curves in the plot folder;
  • save the model with .Rds extension that can be loaded in R using the readRDS function.

The function is totally inspired by the default output of the MaxEnt Java software [@Phillips2006] and extends it to other methods. You can decide what to include in the report using dedicated function arguments, like response_curves, jk and env but the function cannot be used with SDMmodelCV() objects. Run the following code to create a report of the Maxnet model we trained before:

modelReport(maxnet_model, 
            type = "cloglog", 
            folder = "virtual-sp", 
            test = test, 
            response_curves = TRUE, 
            only_presence = TRUE, 
            jk = TRUE, 
            env = predictors)

The output is displayed in the browser and all the files are saved in the virtual-sp folder.

Conclusion

In this article you have learned:

  • how to get and plot the variable importance for Maxent models;
  • how to compute and plot the permutation importance;
  • how to perform the leave one out Jackknife test;
  • how to plot the marginal and the univariate response curve;
  • how to create a model report.

In the next article you will learn how to perform data-driven variable selection.